浮点数的精度丢失问题

浮点数的精度丢失问题 (2023-12-31)

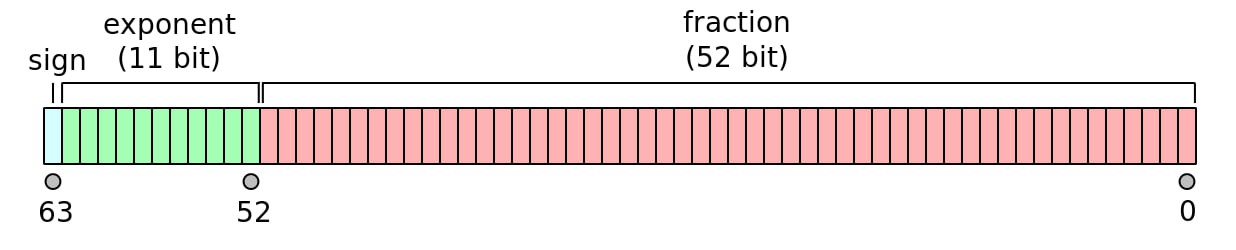
IEEE-754

根据 IEEE 754，浮点数在内存中的存储 (以 double 为例) 表示为 {1个符号位($sign$)+11个指数位($exp$)+52个尾数位($frac$)} 。将各部分的值取出后在 normalized 的形式下它所代表的值 $val$ 可以通过以下式子计算：

$$ val = (-1)^sign \cdot (1 + \sum_{i=0}^{51}b_i * 2^{-(52-i)}) \times 2^{exp-bias}$$

其中 $b_j$ 代表尾数部分从最低位开始的第 $j$ 位上的值。$bias$ 代表的是 IEEE 754 所规定的偏移量，它的值由指数位的大小 $k$ 决定，为 $2^{k-1}-1$，在这个例子中，$bias$ 为 $2^{10}-1 = 1023$。

首先显而易见的，当要存储的信息量超过该浮点类型能存储的最大量 (但指数在合法范围内) 的时候会发生精度丢失。浮点数以类似于科学计数法的方式 (即 $1.101...11_2 \times 2^k$) 存储数值，当小数点后的有效位数超过52位时，会自动进行银行家舍入 (四舍六入，为五则选最近偶数) 保留有效位数为52位，然后丢弃52位以后的所有小数。

此外还有一个不易察觉的问题。观察式子可以发现其所能表示的值的形式可以记作 $\frac{x}{2^k}$ ，这是一个二进制的分数形式。易知分数能写成X进制下的有限小数形式当且仅当其分母可化为X的若干次幂，也即分母的质因数分解必须是X质因数分解的子集。这也意味着一些十进制有限小数是无法表示为二进制下的有限小数的。例如，$1/3$ 可以记为三进制有限小数 $0.1_3$ 和十进制无限循环小数 $0.33…3_{10}$，$1/10$ 可以记为十进制有限小数 $0.1_{10}$，但写成二进制将会是 $0.11001100…1100_2$。这样的无限循环小数被存入浮点数时，超出尾数表示部分的小数会被舍入然后丢弃。

具体的，以 C++ 为例，输出 $0.1$ 的内存表达：

int main() {
  double x = .1;
  auto ptr = (unsigned char *)&x;
  for (int i = 7; i > -1; --i) {
    std::cout << std::format("{:0>8b}", *(ptr+i));;
  }
  return 0;
}

可以得到输出为 (逗号为手动加入)：

$$ 0, 01111111011, 1001100110011001100110011001100110011001100110011010 $$

其中，符号位为 $0$，指数位为 $01111111011_2 = 1019_10$，可得指数应为 $1019 - bias = -4$。

于是整个数可记为 $$2^{-4} \times 1.1001100110011001100110011001100110011001100110011010_2$$，即 $$ 0.100000000000000005551115123126_{10}$$。这里的 $...5551115123126_{10}$ 正是小数点第 52 位后面的 $10011001…_{2}$ 舍入进位带来的。

通常情况下，这不会导致太大的问题。浮点数内部的运算实现与舍入配合的很好。我们可以默认：对于两个浮点数$a, b$之间进行的任意运算 $\odot$，假设其精确(即精度无限大)结果 $x = a \odot b$ ，那么在计算机中得到的结果 $x^{\prime} = Round(a \odot b)$，其中 $Round(y)$ 表示对 y 进行银行家舍入的结果。

但这会要求在一些 tricks 的实现上对细节更加注重。例如一个将浮点数放大 $10^k$ 倍并舍去剩余小数的函数：

long long f(double x, int k) {
  return x * std::pow(10, k);
}

对于这个函数，$f(0.57, 4)$ 的预期结果是 $0.57 * 10^4 = 5700 $。然而实际上该实现得到的是 $5699$。这里的原因是 $0.57_{10}$ 的浮点表示 $0.56999999999999995115_{10}$ 与 $10000_{10}$ 相乘得到的二进制尾数第 53 位为 $0_{2}$ ，然后舍入得到 $5699.99999999999909050530_{10}$。

当然这个问题在目标是提取所有有效小数(移除小数点)的情况下很好解决，只需写成 round(x*pow(10,k)) 或 (int)(x*pow(10,k)+0.1) 即可，其中 $k$ 代表有效小数的位数。这是因为通常情况下放大后的第一位小数要么是 $0$ 要么是 $9$，在舍入的前提下 $9$ 自然代表进位。

Reference

Wikipedia contributors. (2023, December 24). Floating-point arithmetic. Wikipedia. https://en.wikipedia.org/wiki/Floating-point_arithmetic